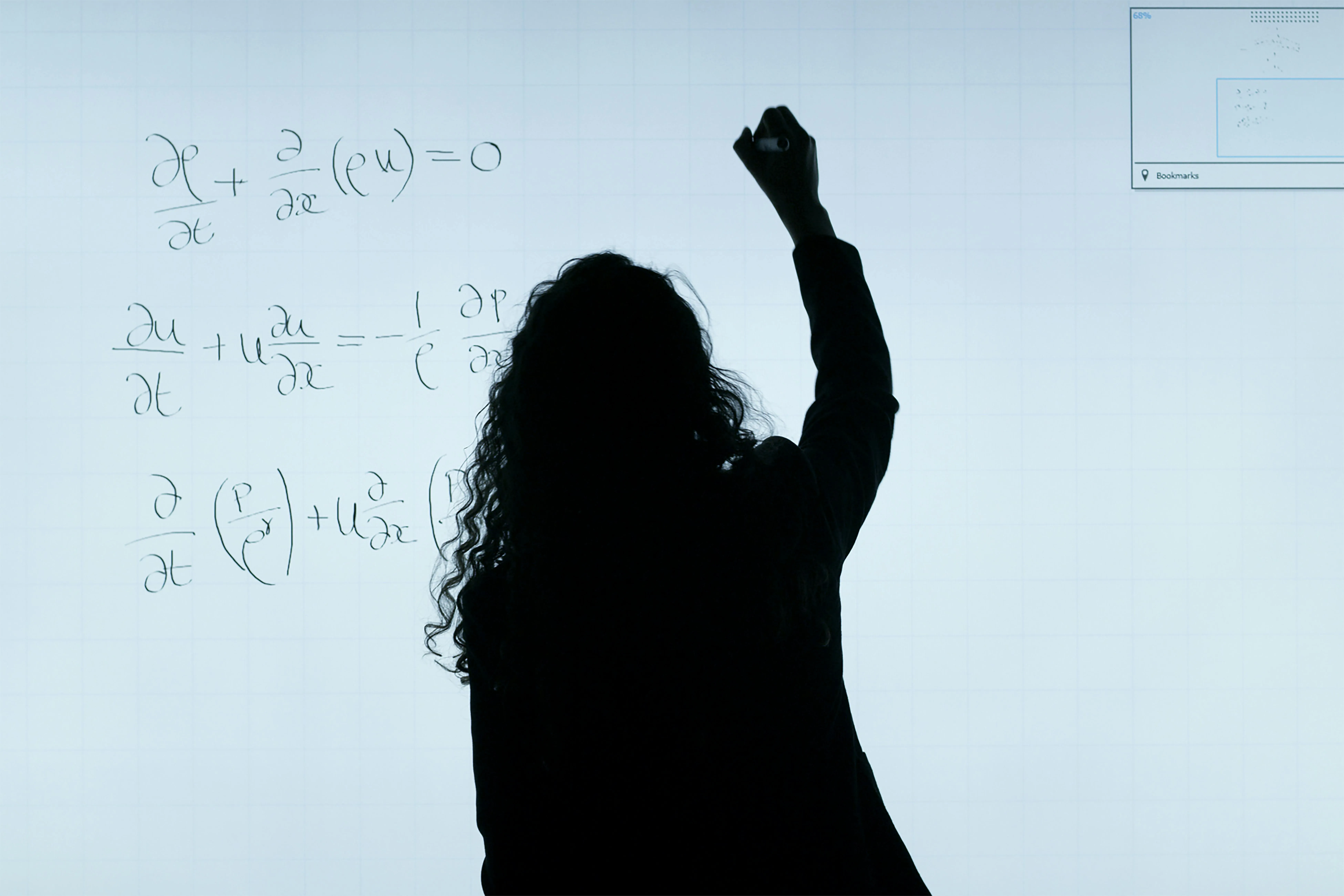Stereometrijos teoremų įrodymas

Pamokoje supažindinama su pagrindinėmis stereometrijos teoremomis ir jų įrodymu. Mokiniai mokosi taikyti stereometrijos teoremas, analizuoti erdvinių figūrų elementų tarpusavio padėtį. Ši pamoka lavina mokinių erdvinį matymą. Praktiniu vaizdo intarpu su Vilniaus Katedros aikšte mokiniams primenama, kad matematikos žinios praverčia ne tik tada, kai reikia kažką apskaičiuoti, bet ir tada, kai patiriamas, arba matomas, vaizdas. Pavyzdžiui, norint pamatyti tikrąjį Katedros aikštėje vaizdą, mums reikia erdvinio, tai yra trimačio, matymo. Erdvinis matymas yra paremtas trimačiu figūrų suvokimu, būtent tai ir nagrinėja stereometrija. Kitas intarpas supažindina su virtualia realybe. Mokiniai sužino, kad daug dalykų iš stereometrijos galima pritaikyti realybėje. O virtuali realybė yra paremta stereometrijos pagrindais, tai yra trimačiu erdvių vaizdavimu. Tad gilindamiesi į stereometriją priartėsime prie galimybės susikurti savo virtualią realybę. Spręsdami uždavinius mokiniai sužino, kad teoremų įrodinėjimas remiasi akivaizdžiomis taškų, tiesių ir plokštumų savybėmis, arba aksiomomis. Primenamos 3 pagrindinės stereometrijos aksiomos.